LES LUTHIERS Y EL TEOREMA DE TALES

El pasado 2 de abril, Beatriz Rubio Serrano vino a nuestro instituto a impartir una charla sobre la aparición de las matemáticas en diferentes campos (cine, prensa, en la red...). Fue muy interesante. Nos pasó una hoja con múltiples enlaces a diferentes páginas web con contenido matemático. En uno de ellos aparecía el siguiente vídeo:

En este vídeo, Les Luthiers, un grupo argentino de humor, que utiliza la música como un elemento fundamental de sus actuaciones, canta sobre el Teorema de Tales. Muchas veces la agrupación utiliza instrumentos informales creados a partir de materiales de la vida cotidiana, (de donde procede su nombre: "luthier" en francés significa "creador de instrumentos musicales"). El grupo fue creado en 1967 por Gerardo Masana, y actualmente sigue en activo.

Tales de Mileto

Tales de Mileto fue un filósofo y científico griego que nació y murió en Mileto, ciudad griega de la costa de Jonia (hoy Turquía). A pesar de que no se conserva ningún fragmento suyo, se le atribuyen importantes aportaciones en el terreno de la filosofía, las matemáticas y la física, entre otros; y se sabe que en la antigüedad era considerado como uno de los Siete Sabios de Grecia.

Este científico y filósofo enunció dos teoremas:

El segundo que postuló dice: 

Sea B un punto de la circunferencia de diámetro AC, distinto de A y de C. Entonces el triángulo ABC, es un triángulo rectángulo.

Segundo teorema de Tales de Mileto

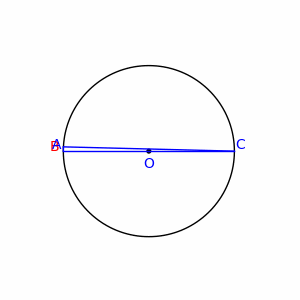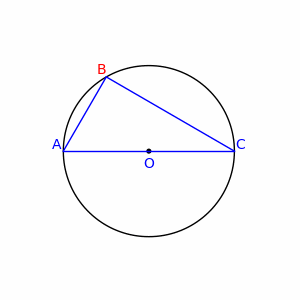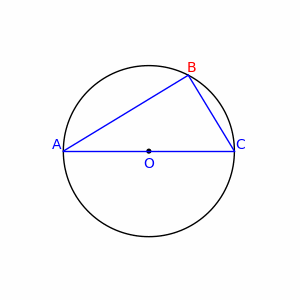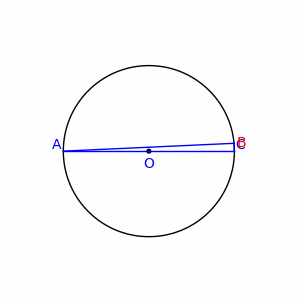Siempre que AC sea un diámetro,
el ángulo B será constante y recto

Y el primero de ellos, del cual habla el vídeo, dice:

Si en un triángulo se traza una línea paralela a cualquiera de sus lados, se obtiene un triángulo que es semejante al triángulo dado.

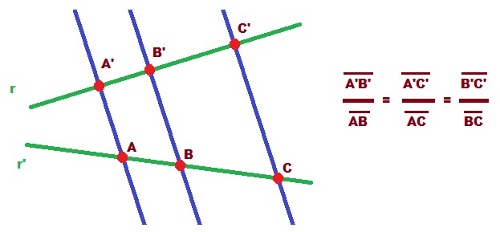Ilustración Teorema de Tales

Según parece, Tales descubrió el teorema mientras investigaba la condición de paralelismo entre dos rectas. Aunque, según la leyenda, fue en un viaje a Egipto, cuando visitó las pirámides de Guiza (las de Keops, Kefrén y Micerino), construidas varios siglos antes. Admirado ante tan portentosos monumentos de esta civilización, quiso saber su altura. Así, trató este problema con semejanza de triángulos. Clavó un palo (de altura conocida) en el suelo, y midiendo la sombra que este proyectaba y la sombra de la pirámide obtuvo dos triángulos rectángulos que pudo relacionar entre sí.

De este modo se cumple que A/B=D/C, por tanto la altura de la pirámide es D= (AC)/B

BIBLIOGRAFÍA:

https://www.youtube.com/watch?v=OXrYNPJQoTA

http://es.wikipedia.org/wiki/Les_Luthiers

http://es.wikipedia.org/wiki/Tales_de_Mileto

http://es.wikipedia.org/wiki/Teorema_de_Tales

http://es.wikipedia.org/wiki/Teorema_de_Tales#Aplicaci.C3.B3n_.28Tales_-_teorema_segundo.29

http://www.profesorenlinea.cl/geometria/Teorema_de_Tales.html